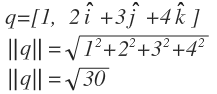Introduction
While crossing a bridge with his wife, Sir William Hamilton made a mathematical discovery so profound he carved it onto a stone. After 10 years of work, he had finally found a way to simultaneously rotate about multiple axis. He named his discovery Quaternions.
Although his discovery went unnoticed for a while, it wasn't until the flight simulation and computer graphics industry that Quaternions mathematics became alive again. Quaternions are mainly used in computer graphics when a 3D character rotation is involved. Quaternions allows a character to rotate about multiple axis simultaneously, instead of sequentially as matrix rotation allows. For example, to rotate 45 degrees about the xy-axis using matrix rotations, the character must first rotate about the x-axis and then rotate about the y-axis. With quaternions this sequential process is not necessary.
Why use Quaternions to rotate a 3D character when matrices can do the same job? There are two reasons why Quaternions are preferred in computer graphics:
- Matrix rotations suffer from what is known as Gimbal Lock.
- Quaternions consume less memory and are faster to compute than matrices.
Gimbal lock is the loss of one degree of freedom in a three-dimensional, three-gimbal mechanism that occurs when the axes of two of the three gimbals are driven into a parallel configuration, "locking" the system into rotation in a degenerate two-dimensional space. 2
The goal to talk about quaternions is to see how they can help us rotate characters more efficiently. However, before we talk about rotations, let's learn a bit more about quaterion arithmetics. .
Quaternions
Quaternions are composed of a scalar and a vector. They are represented in various different ways such as:
where S is a scalar number and V is a vector representing an axis.
Adding and Subtracting
Quaternions can be added and subtracted among themselves. In quaternion addition and subtraction, the corresponding scalar and vectors from each quaternion are added/subtracted, respectively. Mathematically, quaternion addition/subtraction is represented as follows:
For example, the addition of two quaternions is calculated as follows:
Product
Quaternions can be multiplied among themselves. Mathematically, quaternion multiplication is represented as follows:
Scalar Multiplication
Just like vectors and matrices, a quaternion can be multiplied by a scalar. Mathematically, this is represented as follows:
where k is a scalar real number.
Square
The square of a quaternion is given by
For example, the square of quaternion q is calculated as follows:
Norm
Mathematically, the norm of a quaternion is represented as follows:
For example, the norm of quaterion q is calcuated as follows:
Unit Norm
The unit norm of a quaternion, also known as Normalised quaternion, is calculated as follows:
For example, normalizing the quaternion q is calculated as follows:
Conjugate
The conjugate of a quaternion is very important in computing the inverse of a quaternion. Mathematically, the conjugate of quaternion q is calculated as follows:
Inverse
The ability to divide in quaternion arithmetic is very important. To be able to divide a quaternion, you need its inverse. By definition the inverse quaternion satisfies the following:
The inverse of a quaternion is defined as:
Reference: Quaternions for Computer Graphics by John Vince