A math engine contains functions which allows a 3D object to translate and rotate. It consists of the following C++ classes:

Vectors
Matrix
Quaternions

Vectors translate a 3D object. Whereas, matrices and quaternions rotate a 3D object.

In this post, you will learn about vectors and how to implement them in C++. In the next post, you will learn about matrices and how they are implemented in code.

Let's begin:

Creating a Command-Line project

We will be implementing the Math Engine using Apple's Xcode IDE. The plan is to implement the math engine in Xcode and test it using the command line.

Step 1:

Let's create a command-line project in Xcode. Open up Xcode, click on New and select Project. Under the OS X section select Application and click on Command Line Tool as shown below.

Creating a Command Line Tool application in Xcode

Step 2:

Next, name your project. I will be naming this engine Revolved 4D Math Engine.

Step 3:

Xcode should have generated a simple .cpp main file. Our next step is to create a Vector class. To do so, right-click on your project name and select New File. Select the C++ File option as shown below.

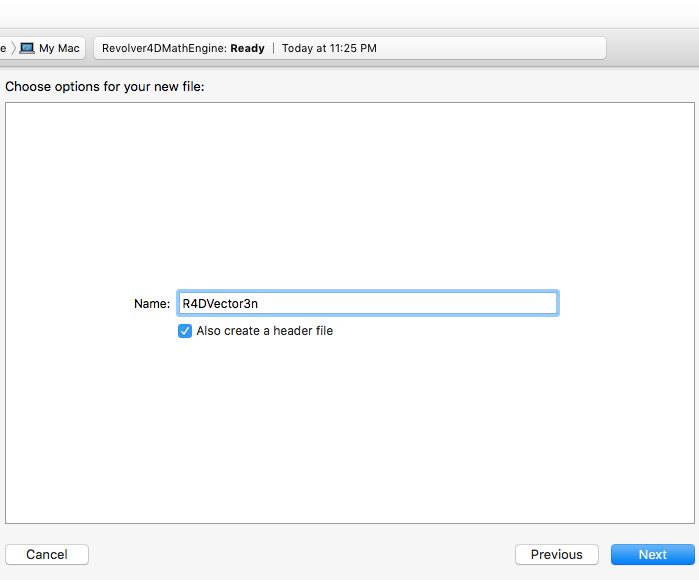
Step 4:

Name your file R4DVector3n.

Xcode will create a R4DVector3n.cpp and R4DVector3n.h file with this name.

Step 5:

Our goal is to use this math engine in iOS devices. iOS applications are programmed using the Objective-C language. However, the math engine we will be developed using C++. In order for the .cpp & .hpp file to be compile under an iOS application, we need to change the file extensions.

Change the .cpp extension to .mm and change the .hpp extension to .h. This modification is show below.

Namespace

Namespaces prevent clashes with any other library that could be using the same function/method names. To avoid any clashes, our math library will employ the following namespace:

namespace R4DEngine{}

All classes of our math engine will be referenced through this namespace. I will explain how this is done once we implement the Vector class.

Vectors

We are ready to start implementing our vector class in code. But first, let's review what a vector is.

A vector is composed of N number of components. The number of components determines the dimension of the vector. A three-dimensional vector contains three components defining a displacement along the x, y and z axis. Mathematically, a three-dimensional vector is defined as:

A vector class can be defined as follows:

Listing 1. Vector class

namespace R4DEngine {
    class R4DVector3n{

    private:

    public:
        //x, y and z dimensions
        float x;
        float y;
        float z;

        //Constructors
        R4DVector3n();
        R4DVector3n(float uX,float uY,float uZ);

        //Destructors
        ~R4DVector3n();

        //Copy Constructors
        R4DVector3n(const R4DVector3n& v);
        R4DVector3n& operator=(const R4DVector3n& v);     
      };
}

Notice that the data members x, y and z are public data members instead of private members. Doing so makes working with the engine a lot more cleaner. Please read Tips on developing a Math Engine for more information.

In the definition class (.mm) the constructor and copy constructors are defined as follows:

namespace R4DEngine {

//constructor
    R4DVector3n::R4DVector3n():x(0.0),y(0.0),z(0.0){};

    R4DVector3n::R4DVector3n(float uX,float uY,float uZ):x(uX),y(uY),z(uZ){}

//destructor
    R4DVector3n::~R4DVector3n(){}

//copy constructor     
    R4DVector3n::R4DVector3n(const R4DVector3n& v):x(v.x),y(v.y),z(v.z){}

    R4DVector3n& R4DVector3n::operator=(const R4DVector3n& v){

        x=v.x;
        y=v.y;
        z=v.z;

        return *this;

    }

}

Let's test what we have. In the main.mm file, type the following:

#include <iostream>
#include "R4DVector3n.h"

int main(int argc, const char * argv[]) {

    //declare two vectors. Notice that I'm referencing the namespace
    R4DEngine::R4DVector3n vector1(2,3,1);
    R4DEngine::R4DVector3n vector2(1,2,0);

    return 0;
}

Press Command+B. You should get a successful build. The output window should show the components of each vector.

Addition/Subtraction

Addition

In vector addition, each vector component are individually added to the corresponding component in the second vector. Vector addition is represented mathematically as:

For example, adding two three-dimensional vectors is done as follows:

We will implement vector addition by overloading C++ operators.

Our vector addition methods will look as follows:

void R4DVector3n::operator+=(const R4DVector3n& v){
    //Resultant of two vectors
    x+=v.x;
    y+=v.y;
    z+=v.z;
}

R4DVector3n R4DVector3n::operator+(const R4DVector3n& v)const{
    //Returns a third vector representing the addition of two 3D vectors
    return R4DVector3n(x+v.x,y+v.y,z+v.z);
}

Let's test what we have. In the main.mm file, type the following:

#include <iostream>
#include "R4DVector3n.h"

int main(int argc, const char * argv[]) {

    R4DEngine::R4DVector3n vector1(2,3,1);
    R4DEngine::R4DVector3n vector2(1,2,0);

    //adding: vector3=vector1+vector2

    R4DEngine::R4DVector3n vector3=vector1+vector2;

    //adding: vector1+=vector2

    vector1+=vector2;

    return 0;
}

Press Command+B. You should get a successful build. The output window should show the vector addition results.

Subtraction

In vector subtraction, the components of the vectors are subtracted from each other. Vector subtraction is represented mathematically as:

For example, subtracting two three-dimensional vectors is done as follows:

The implementation of vector subtraction is as follows:

void R4DVector3n::operator-=(const R4DVector3n& v){

    x-=v.x;
    y-=v.y;
    z-=v.z;
}

R4DVector3n R4DVector3n::operator-(const R4DVector3n& v)const{

    return R4DVector3n(x-v.x,y-v.y,z-v.z);
}

Let's test these methods in main.mm

#include <iostream>
#include "R4DVector3n.h"

int main(int argc, const char * argv[]) {

    R4DEngine::R4DVector3n vector1(2,3,1);
    R4DEngine::R4DVector3n vector2(1,2,0);

    //subtraction: vector3=vector1-vector2

    R4DEngine::R4DVector3n vector3=vector1-vector2;

    //subtraction: vector1-=vector2

    vector1-=vector2;

    return 0;
}

Press Command+B and review the result of the subtraction operations in the output window:

Scalar multiplication/division

Geometrically, multiplying a vector with a scalar streches the length of a vector. Dividing a vector by a scalar has the opposite effect. To multiply a vector by a scalar, simply multiply each component by the scalar. Note that multiplying a vector by a positive scalar only affects its magnitude. However, multiplying it by a negative scalar affects its magnitude and reverses its direction. Scalar multiplication is represented mathematically as:

For example, scaling a vector by 3 is done as follows:

Scalar multiplication and Scalar division is implemented as follows:

void R4DVector3n::operator*=(const float s){
    x*=s;
    y*=s;
    z*=s;
}

R4DVector3n R4DVector3n::operator*(const float s) const{
    return R4DVector3n(s*x,s*y,s*z);
}

//divide by scalar
void R4DVector3n::operator /=(const float s){
    x=x/s;
    y=y/s;
    z=z/s;
}

R4DVector3n R4DVector3n::operator/(const float s)const{
    return R4DVector3n(x/s,y/s,z/s);
}

Let's make sure these methods work by testing them in main.mm.

#include "R4DVector3n.h"

int main(int argc, const char * argv[]) {

    R4DEngine::R4DVector3n vector1(2,3,1);
    R4DEngine::R4DVector3n vector2(1,2,0);

    //multiplication: vector3=5.0*vector2

    R4DEngine::R4DVector3n vector3=vector2*5.0;

    //multiplication: vector1*=7.0

    vector1*=7.0;

    //division: vector4=5.0/vector2
    R4DEngine::R4DVector3n vector4=vector2/5.0;

    //division: vector2/=7.0
    vector2/=7.0;

    return 0;
}

The output window should produce the following results:

Vector Scalar multiplication & Scalar division

Vector Product

Unlike real numbers, vectors do not have a single multiplication operation. They have two distinct type of product operations; the dot product and cross product. The dot product produces a scalar and is mainly use to determine the angle between vectors. The cross product produces a vector perpendicular to the multiplicand and multiplier vectors.

Dot Product The Dot Product is a vector operation that calculates the angle between two vectors. The dot product is calculated in two different ways.

Version 1

In the above equation, information about the angle between the vectors is missing. However, the result from this equation can tell us the direction of each vector. For example, if the dot product is equal to 1, it means that both vectors have the same direction. If the dot product is 0, it means that both vectors are perpendicular on each other. Finally, if the dot product is -1, it means that both vectors are heading in opposite directions.

Version 2

If we are interested in finding the angle between two vectors, the dot-product equation below can be used.

The dot product can be implemented in code as follows:

float R4DVector3n::operator*(const R4DVector3n& v) const{
    return x*v.x+y*v.y+z*v.z;
}

float R4DVector3n::dot(const R4DVector3n& v) const{
    return x*v.x+y*v.y+z*v.z;
}

Let's test the dot product between two vectors in main.mm:

#include "R4DVector3n.h"
int main(int argc, const char * argv[]) {

    R4DEngine::R4DVector3n vector1(2,3,1);
    R4DEngine::R4DVector3n vector2(1,2,0);

    //dot product
    float dotProduc1=vector1.dot(vector2);
    float dotProduct2=vector1*vector2;  
    return 0;
}

Let's run the code and see the results in the output window:

Cross Product

Two vectors produces a plane. A cross product operation produces a vector that is perpendicular to both vectors. The cross product of two vectors is calculated as follows:

It is important to remember that a cross product can only be calculated with vectors in three-dimensions. If vectors reside in two-dimensional space, and the cross product is required, the vectors must be converted to three-dimensional vectors.

The cross product can be implemented as follows:

R4DVector3n R4DVector3n::cross(const R4DVector3n& v) const{

    return R4DVector3n(y*v.z-z*v.y,
                       z*v.x-x*v.z,
                       x*v.y-y*v.x);
}

void R4DVector3n::operator %=(const R4DVector3n& v){
    *this=cross(v);
}

R4DVector3n R4DVector3n::operator %(const R4DVector3n& v) const{
    return R4DVector3n(y*v.z-z*v.y,
                       z*v.x-x*v.z,
                       x*v.y-y*v.x);
}

You can test the cross product in three different ways in main.mm:

#include "R4DVector3n.h"

int main(int argc, const char * argv[]) {

    R4DEngine::R4DVector3n vector1(2,3,1);
    R4DEngine::R4DVector3n vector2(1,2,0);

    //cross product
    R4DEngine::R4DVector3n vector3=vector1.cross(vector2);

    R4DEngine::R4DVector3n vector4=vector1%vector2;

    vector1%=vector2;


    return 0;
}

Build the project and review the cross product results in the output window:

Magnitude of a vector

A vector magnitude represents the length of a vector. The length of a vector is calculated as follows:

For example, the magnitude of vector u is done as follows:

float R4DVector3n::magnitude(){

    float magnitude=std::sqrt(x*x+y*y+z*z);

    return magnitude;

}

Let's test this method in main.mm:

#include "R4DVector3n.h"

int main(int argc, const char * argv[]) {

    R4DEngine::R4DVector3n vector1(2,3,1);

    //magnitude
    float magnitude=vector1.magnitude();

    return 0;
}

Press Command+B. The output window should show the following result:

Unit vector

A very useful concept in computer graphics is what is known as a unit vector. A unit vector is a vector with length of 1 unit. The process of convertion a non-unit vector to a unit vector is called Normalization. To normalize a vector, each component is divided by the length of the vector. Mathematically this is represented as:

The normalization of vector u is done as follows:

void R4DVector3n::normalize(){

    float mag=std::sqrt(x*x+y*y+z*z);

    if (mag>0.0f) {

        //normalize it
        float oneOverMag=1.0f/mag;

        x=x*oneOverMag;
        y=y*oneOverMag;
        z=z*oneOverMag;   
    }
}

The normalization of a vector is perform as shown below:

#include "R4DVector3n.h"

int main(int argc, const char * argv[]) {

    R4DEngine::R4DVector3n vector1(2,3,1);

    //normalize the vector
    vector1.normalize();

    return 0;
}

Press Command+B and review the normalization of the vector in the output window:

Source Code

The complete source code can be found here. Feel free to download it and play with it.

Developing a Math Engine in C++: Implementing Vectors