In the previous post, you learned how to shade a 3D model. The shading effect was very simple. It merely provided the 3D model with a depth-perception. In this post, you will learn how to light an object by simulating Ambient-Diffuse-Specular (ADS) Lighting.
Before I start, I recommend you to read the prerequisite materials listed below:
Prerequisite:
How Light Works?
When light rays hit an object, the rays are either reflected, absorbed or transmitted. For our discussion, I will focus solely on light rays reflection.
When a light ray hits a smooth surface, the ray will be reflected at an angle equal to its incident ray. This type of reflection is known as Specular Reflection.
Visually, specular reflection is the white highlight seen on smooth, shiny objects.
In contrast, when a light ray hits a rough surface, the ray will be reflected at a different angle as its incident ray. This type of reflection is known as Diffuse Reflection.
Diffuse reflection enables our brain to make out the shape and the color of an object. Thus, diffuse reflection is more important to our vision than specular reflection.
Let's go through a simple animation to understand the difference between these reflections.
The animation below shows a 3D model with only specular reflection:
Whereas, the animation below shows a 3D model with only diffuse reflection:
As you can see, it is almost impossible for our brain to make out the shape of an object with only specular reflection.
There is another type of reflection known as Ambient Reflection. Ambient reflection is light rays that enter a room and bounces multiple types before reflecting off a particular object.
When we combine these three types of reflections, we get the following result:
Simulating Light Reflections
Now that you know how light works, the next question is: How can we model it mathematically?
Diffuse Reflection
In diffuse reflection, a light ray's reflection angle is not equal to its incident angle. From experience, we also know that a light ray's incident angle influences the brightness of an object. For example, an object will have different brightness when a light ray hits the object's surface at a 90-degree angle than when light rays hit the surface at a 5-degrees angle.
Mathematically, we can simulate this natural behavior by computing the Dot-Product between the light rays and a surface's Normal vector. When a light source vector S is parallel and heading in the same direction as the normal vector n, the dot product is 1, meaning that the surface location is fully lit. Recall, the dot product ranges between [-1.0,1.0].
As the light source moves, the angle between vectors S and n changes, thus changing the dot product value. When this occurs, the brightness levels also changes.
Taking into account the surface's Diffuse Reflection factor, the equation for Diffuse Reflection is:
Specular Reflection
In Specular Reflection, the light ray's reflection angle is always equal to its incident angle. However, the specular reflection that reaches your eyes is dependent on the angle between the reflection ray (r) and the viewer's location (v).
This behavior implies that to model a specular reflection; we need to compute a reflection vector from a normal vector and the light ray vector. We then calculate the influence of the reflection's vector onto the viewer's vector, i.e., we compute the dot product. The result provides the specular reflection of the object.
Taking into account the surface's Specular Reflection factor, the equation for Specular Reflection is:
The exponent determines the size of the highlight.
Ambient Reflection
There is not much to ambient reflection. The ambient reflection depends on the light’s ambient color and the ambient’s material reflection factor.
The equation for Ambient Reflection is:
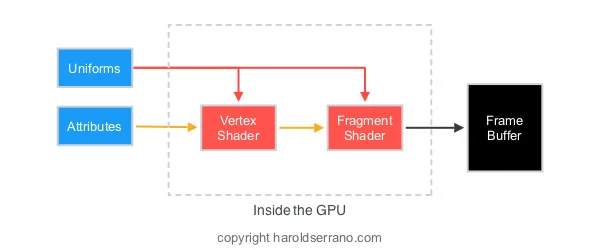
Simulating Light in the Rendering Pipeline
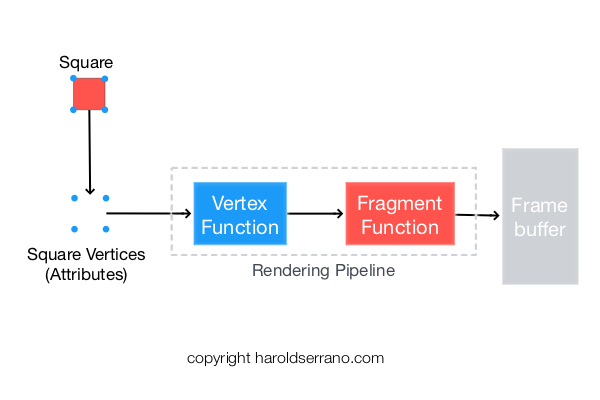
In Computer Graphics, Light is simulated in either the Vertex or Fragment Shaders. When lighting is simulated in the Vertex Shader, it is known as Gouraud Shading. If lighting is simulated in the Fragment Shader, it is known as Phong Shading.
Gouraud shading (AKA Smooth Shading) is a per-vertex color computation. What this means is that the vertex shader determines the lighting for each vertex and pass the lighting results, i.e. a color, to the fragment shader. Since this color is passed to the fragment shader, it is interpolated across the fragments thus giving the smooth shading.
Here is an illustration of the Gouraud Shading:
In contrast, Phong shading is a per-fragment color computation. The vertex shader provides the normal vectors and position data to the fragment shader. The fragment shader then interpolates these variables and calculates the lighting for the fragment.
Here is an illustration of the Phong Shading:
With either, Gouraud or Phong Shading, the Lighting computation is the same, although the results will differ.
In this project, we will implement a Phong Shading Light effect. For your convenience, I provide link to the Gouraud Shading Light project at the end of the article.
Setting up the project
Let's apply Lighting (Phong shading) to a 3D model.
By now, you should know how to set up a Metal Application and how to implement simple shading to a 3D object. If you do not, please read the prerequisite articles mentioned above.
For your convenience, the project can be found here. Download the project so you can follow along.
Note: The project is found in the "applyingLightFragmentShader" git branch. The link should take you directly to that branch. Let's start,
Open up file "MyShader.metal"
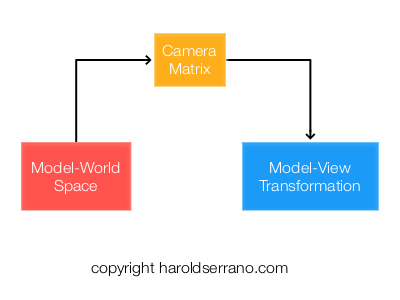
The only operation we do in the Vertex Shader is to pass the normal vectors and vertices (in Model-View Space) to the fragment shader as shown below:
//6. Pass the vertices in MV space
vertexOut.verticesInMVSpace=verticesInMVSpace;
//7. Pass the normal vector in MV space
vertexOut.normalVectorInMVSpace=normalVectorInMVSpace;
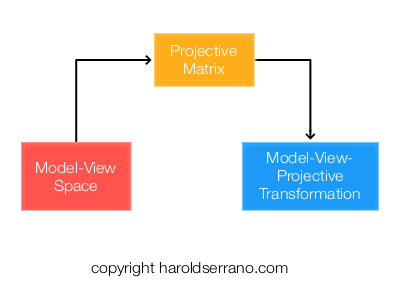
In the fragment shader, the first thing we do is to compute the light ray vector as shown below:
//2. Compute the direction of the light ray betweent the light position and the vertices of the surface
float3 lightRayDirection=normalize(lightPosition.xyz-vertexOut.verticesInMVSpace.xyz);
We then compute the reflection vector between the light ray vector and the normal vectors as shown below:
//4. Compute reflection vector
float3 reflectionVector=reflect(-lightRayDirection,vertexOut.normalVectorInMVSpace);
The diffuse reflection is computed by first computing the diffuse intensity between the normal vectors and the light ray vector. The diffuse intensity is then multiplied by the light color and the material diffuse reflection factor. The snippet below shows this calculation:
//6. compute diffuse intensity by computing the dot product. We obtain the maximum the value between 0 and the dot product
float diffuseIntensity=max(0.0,dot(vertexOut.normalVectorInMVSpace,lightRayDirection));
//7. compute Diffuse Color
float3 diffuseLight=diffuseIntensity*light.diffuseColor*material.diffuseReflection;
To compute the specular reflection, we take the dot product between the reflection vector and the view vector. This factor is then multiplied by the specular light color and the material specular reflection factor.
//8. compute specular lighting
float3 specularLight=float3(0.0,0.0,0.0);
if(diffuseIntensity>0.0){
specularLight=light.specularColor*material.specularReflection*pow(max(dot(reflectionVector,viewVector),0.0),material.specularReflectionPower);
}
The total lighting reflection color is then added together and is assign to the fragment:
//9. Add total lights
float4 totalLights=float4(ambientLight+diffuseLight+specularLight,1.0);
//10. assign light color to fragment
return float4(totalLights);
You can now build and run the project. However, since you have a texture applied to the 3D model, you can mix the lighting color with the sampled texture color, as shown below:
//10. set color fragment to the mix value of the shading and light
return float4(mix(sampledColor,totalLights,0.5));
And that is it, build the project. Swipe your finger across the screen; you should see the lighting change as you move your fingers.
ADS Phong Shading