In the previous article, you learned how to render a 3D object. However, the object lacked depth perception. In computer graphics, as in art, shading depicts depth perception by varying the level of darkness.
Before I start, I recommend you to read the prerequisite materials listed below:
Prerequisite:
Shading
As mentioned in the introduction, shading depicts depth perception by varying the level of darkness on an object. For example, the image below shows a 3D model without any depth perception:
Whereas, the image below shows the 3D model with shading applied:
The shading levels are dependent on the incident angle between the surface and light rays. For example, an object will have different shading when a light ray hits the object's surface at a 90-degree angle than when light rays hit the surface at a 5-degrees angle. The image below depicts this behavior; the shading effects vary depending on the angle between the light source and the surface.
We can simulate this natural behavior by computing the Dot-Product between the light rays and a surface's Normal vector. When a light source vector s is parallel and heading in the same direction as the normal vector n, the dot product is 1, meaning that the surface location is fully lit. Recall, the dot product ranges between [-1.0,1.0].
As the light source moves, the angle between vectors s and n changes, thus changing the dot product value. When this occurs, the shading levels also changes.
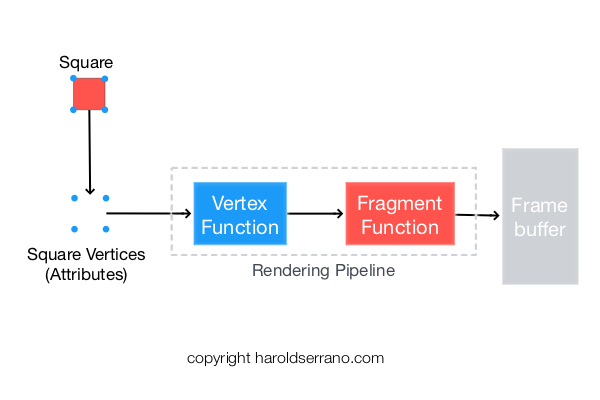
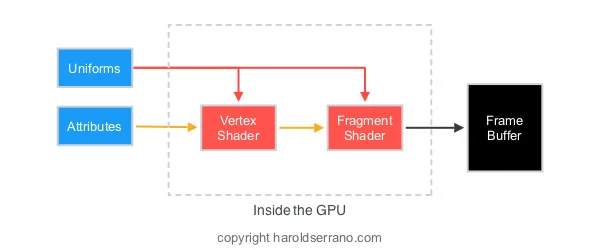
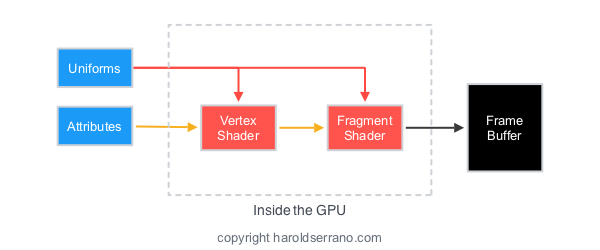
Shading is implemented either in the Vertex or Fragment Shaders (Functions), and it requires the following information:
- Normal Vectors
- Normal Matrix
- Light Position
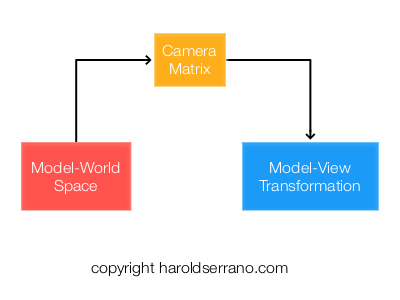
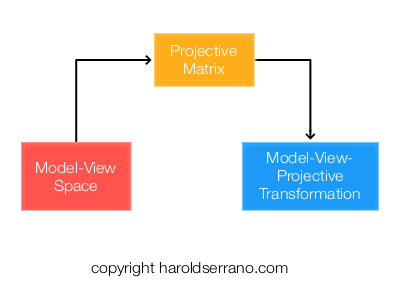
- Model-View Space
Normal vectors are vectors perpendicular to the surface. Luckily, we don't have to compute these vectors. This information is supplied by any 3D modeling software such as Blender.
The Normal Matrix is extracted from the Model-View Space transformation and is used to transform the normal vectors. The Normal Matrix requires being transposed and inverted before they can be used in shading.
The light position is the location of the light source in the scene. The light position must be transformed into View Space before you can shade the object. If you do not, you may see weird shading.
We will implement shading in the Vertex Shader (Function). In our project, the Normal Vectors will be passed down to the vertex shader as attributes. The Normal Matrix and light position will be passed down as uniforms.
Setting Up the Application
Let's apply shading to a 3D model.
By now, you should know how to set up a Metal Application and how to render a 3D object. If you do not, please read the prerequisite articles mentioned above. In this article, I will focus on setting up the Shaders.
For your convenience, the project can be found here. Download the project so you can follow along.
Note: The project is found in the "shading3D" git branch. The link should take you directly to that branch.
Let's start,
By now, you should know how to pass attribute and uniform data to the GPU using Metal, so I will not go into much detail.
Also, the project is interactive. As you swipe your fingers across the screen, the x and y coordinates of the light source will change. Thus a new shading value will be computed every time you touch the screen.
Open up the "ViewController.mm" file.
The project contains a method called "updateTransformation" which is called before each render pass. In the "updateTransformation" method, we are going to compute the Normal Matrix space and transform the new light position into the Model-View space. This information is then passed down to the vertex shader.
Updating Normal Matrix Space
The Normal Matrix space is extracted from the Model-View transformation. Before each render pass, the Normal Matrix must be transposed and inverted as shown in the snippet below:
//get normal matrix
matrix_float3x3 normalMatrix={modelViewTransformation.columns[0].xyz,modelViewTransformation.columns[1].xyz,modelViewTransformation.columns[2].xyz};
normalMatrix=matrix_transpose(matrix_invert(normalMatrix));
//load the NormalMatrix into the MTLBuffer
normalMatrixUniform=[mtlDevice newBufferWithBytes:(void*)&normalMatrix length:sizeof(normalMatrix) options:MTLResourceOptionCPUCacheModeDefault];
Updating Light Position
The position of the light source is transformed into the View space before each render pass. See the snippet below:
//light position
vector_float4 lightPosition={xPosition*5.0,yPosition*5.0+10.0,-5.0,1.0};
// transform the light position
lightPosition=matrix_multiply(viewMatrix, lightPosition);
// load the light position into the MTLBuffer
mvLightUniform=[mtlDevice newBufferWithBytes:(void*)&lightPosition length:sizeof(lightPosition) options:MTLResourceCPUCacheModeDefaultCache];
Setting up the Shaders
Open up the "MyShader.metal" file.
We will implement shading in the Vertex Shader. The Vertex Shader (Function) receives the following information in its argument:
- Normal Vectors (as attributes)
- Model-View space
- Normal Matrix Space
- Light Position
To apply shading, we transform the Normal Vectors into Normal Matrix space as shown below:
//2. transform the normal vectors by the normal matrix space
float3 normalVectorInMVSpace=normalize(normalMatrix*normal[vid].xyz);
Since we need to compute the light ray direction, we transform the model's vertices into the same space as the Light Position, i.e., we transform it into the Model-View space. Once this operation is complete, we can compute the light ray direction by subtracting the light position and the surface vertices. See the snippet below:
//3. transform the vertices of the surface into the Model-View Space
float4 verticesInMVSpace=mvMatrix*vertices[vid];
//4. Compute the direction of the light ray betweent the light position and the vertices of the surface
float3 lightRayDirection=normalize(lightPosition.xyz-verticesInMVSpace.xyz);
With the Normal Vectors and the light ray direction, we can compute the intensity of the shading. Since the dot product ranges from [-1,1], we get the maximum value between 0 and the dot product as shown below:
//5. compute shading intensity by computing the dot product. We obtain the maximum the value between 0 and the dot product
float shadingIntensity=max(0.0,dot(normalVectorInMVSpace,lightRayDirection));
Next, we multiply the shading intensity value, by a particular light color. The shading color is then passed down to the fragment shader (function).
//6. Multiply the shading intensity by a light color
float4 shadingColor=shadingIntensity*lightColor;
//7. Pass the shading color to the fragment shader
vertexOut.color=shadingColor;
The fragment shader is quite simple. It applies the shading color to the 3D model.
And that is it. Build the project and swipe your finger across the screen. The 3D object will be shaded differently depending on the position of the light source.
Note: As of today, the iOS simulator does not support Metal. You need to connect your iPad or iPhone to run the project.
Hope this helps