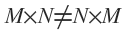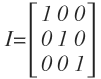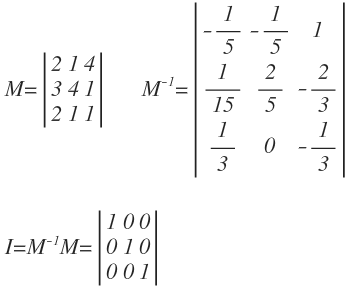Introduction
The usefulness of a matrix in computer graphics is its ability to convert geometric data into different coordinate systems. A matrix is composed of elements arranged in rows and columns. In simple terms, the elements of a matrix are coefficients that represents the scale or rotation a vector will undergo during a transformation.
Matrix
A matrix is an entity composed of components arranged in rows and columns. Mathematically, a matrix is represented as:
The rows and columns of a matrix determines the dimension of a matrix. A matrix containing 2 rows and 3 columns is of dimension 2x3. Here is an example of matrices with different dimensions:
Dimensions in matrix arithmetic is very important, since some operations are not possible unless matrices have identical dimensions. Matrices can be added and subtracted. They can be multiplied by a scalar and multiplied among themselves. Matrices can not be divided, instead a matrix called the Inverse is calculated which serves as the reciprocal of the matrix. Matrices have an arrangement property. They can be arranged in row-major format or column-major format. This is very important to keep in mind since multiplying vectors or matrices of wrong format will result in wrong calculations. OpenGL requires all matrices to be in column-major format
Addition/Subtraction
Matrix addition/subtraction is allowed between matrices that have the same dimension. To add matrices simply add the corresponding component to each other.
For example:
Scalar Multiplication
Scalar multiplication is performed by multiplying a scalar with each corresponding component in the matrix.
For example:
Multiplication
Unlike matrix addition, matrix multiplication does not require matrices to be of the same dimensions. However, the number of rows in matrix M must be equal to the number of colums in matrix N. For example:
For example:
Note, an important propertry of matrices:
Thus, be careful when multiplying matrices. The order of multiplication matters.
Identity Matrix
The Identity Matrix is a special kind of matrix which is similar to the concept of “1” in real numbers. Just like a real number multiplied by “1” results in the real number itself, any matrix multiply by the identity matrix results in the matrix itself. The Identity matrix is defined as:
Multiplying any matrix by the identity matrix results in the same matrix.
Inverse
In arithmetic, dividing a number by “4” is the same as multiplying a number by the inverse of “4”, i.e., “1/4”. Division operation does not exist in matrix arithmetic. However, it is possible to multiply a matrix by an inverse. The inverse of a matrix is denoted as:
When a matrix is multiplied by its inverse, it produces an identity matrix. Similar to when the real number “4” is multiplied by its inverse “1/4” produces “1”.
Keep in mind that not all matrices have an inverse.
Transpose
A Transpose operation takes each row of a matrix and converts it to a corresponding column. Mathematically, a transpose is represented as:
For example, the transpose of matrix M is done as follows:
Why would you need to transpose a matrix? A matrix can be represented as either a row-major or column-major matrix. During transformation operations, a vector and a matrix must be in either the same row-major or colum-major format. If they are not, the matrix must be transpose, so the results of the transformation are correct.