A physics engine is responsible for solving the equation of motion and for detecting collisions. You can think of a physics engine as a continuous loop. It starts off by simulating an external force such as gravity. At each new time step, it detects any collisions, then calculates the velocity and position of an object. And finally, sends the location data to the GPU. This continuous loop creates the illusion that an object is falling due to gravity.
Physics Engine Loop
The Physics engine is responsible for computing the resulting accelerations, velocity, and displacement of an object from forces and torques acting on the body.
In Physics engine development, the most important equations are:
Newton's second law:
Rotational Force (Moments, Torque):
These two equations are known as the Equations of Motion.
Recall that if you integrate acceleration with respect to time, you obtain velocity. If you integrate velocity with respect to time, you get displacement.
The Physics Engine integrates the Equation of Motion to obtain the resultant velocity and displacement of an object. And it does this in a continuous loop which consists of the following steps:
- Identify all forces and moments acting on the object.
- Take the vector sum of all forces and moments.
- Solve the equation of motion for linear and angular acceleration.
- Integrate the acceleration with respect to time to find the linear and angular velocity.
- Integrate the velocity with respect to time to find the linear and angular displacement.
If a gravitational force and torque are applied to an object, the Physics Engine loop creates the illusion that an object falls and rotates.
Numerical Integration
In computers, Integrals are evaluated using Numerical Integration. The reason is that computers can only approximate the value of an integral by using numerical techniques.
There are several numerical integration techniques used for solving the equation of motion. The most common are:
- Euler Method
- Verlet Method
- Runge-Kutta Method
The Euler Method is simple to implement but is the least exact. The Runge-Kutta method is complicated to implement but the most precise.
Collision Detection
Although collision detection is a responsibility of the physics engine, this responsibility is delegated to a Collision Detection system. Both of these systems work hand in hand to determine collision. For simplicity, I will not make a distinction between these systems in this article.
The goal of a collision detection system is to report if two objects have collided. It reports a simple YES/NO answer. However, this operation is extremely time-consuming. The physics engine, to speed up collision detection, divides the process into a Broad-Phase and a Narrow-Phase.
Broad Phase Collision Detection
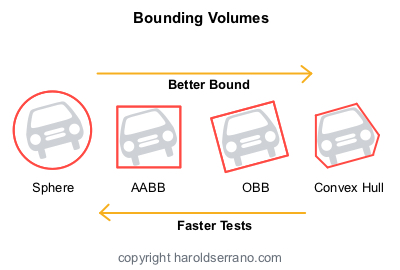
As the physics engine hands down objects to the collision system, the objects are wrapped with bounding volumes. The most traditional bounding volumes are Spheres, Axis-Aligned Bounding Boxes (AABB), and Oriented Bounding Boxes (OBB).
During the Broad-Phase Collision Detection, every object is wrapped with a Sphere bounding volume. The physics engine parses the space of every object and creates a Boundary Volume Hierarchy (BVH). The BVH produces a tree-like structure where each node contains objects that are most likely to collide.
The physics engine tests each node and creates a list of collision pairs. The Broad Phase is fast, and it may report false positives collisions. But even so, it removes all non-possible collision pairs.
A sphere-sphere collision is faster to detect than an OBB-OBB collisions. However, it does report false positives.
Narrow Phase Collision Detection
The collision-pair list is then passed down to the Narrow Phase Collision Detection. In this phase, each object is wrapped with a Convex Hull Volume approximating its shape. The collision detection then performs a collision test between these convex hulls using the Gilbert-Johnson-Keerthi (GJK) algorithm. This algorithm is precise but expensive.
Collision Response
A collision response calculates the resulting velocities (linear and angular) of the objects after colliding and instantly changes their velocities accordingly. This calculation requires information such as mass, a coefficient of restitution, collision points, and collision-normal vector.
At the instant of collision, the most significant force acting on the objects is the collision force (Impact force), so all other forces are ignored for that instant. The impact force is high in magnitude but short in duration.
After a collision, the impact force dies out, and external forces act on the object once again. The equation of motion is solved, providing a new position and velocity. The physics engine performs this process continuously, and it creates the illusion that an object is falling due to gravity.
The purpose of a physics engine is to solve the equation of motion and detect collisions. The goal is simple to understand yet complicated to implement.
PS. Sign up to my newsletter and get Game Engine development tips.