A math engine requires the implementations of:
- Vectors
- Matrices
- Quaternions
My previous post explained how vectors are implemented in a math engine. This post will go into the implementation of matrices. Matrices are used to rotate, scale and skew 3D objects.
Let's begin.
Prerequesite: I strongly encourage to read how vectors are implemented in C++ before reading this article.
This post is part of Developing a Rendering Engine project. Learn more here.
Matrix
A matrix is an entity composed of components arranged in rows and columns. Mathematically, a matrix is represented as:
The rows and columns of a matrix determines the dimension of a matrix. A matrix containing 2 rows and 3 columns is of dimension 2x3. Here is an example of matrices with different dimensions:
Dimensions in matrix arithmetic is very important, since some operations are not possible unless matrices have identical dimensions. Matrices can be added and subtracted. They can be multiplied by a scalar and multiplied among themselves. Matrices can not be divided, instead a matrix called the Inverse is calculated which serves as the reciprocal of the matrix.
Creating Matrix Class
Let's create a Matrix class in our math engine. Download the math engine and create a new class called R4DMatrix3n.
Our goal is to use this math engine in iOS devices. iOS applications are programmed using the Objective-C language. However, the math engine we will be developed using C++. In order for the .cpp & .hpp file to compile under an iOS application, we need to change the file extensions.
Change the .cpp extension to .mm and change the .hpp extension to .h
A Matrix class is defined as follows:
namespace R4DEngine {
class R4DMatrix3n{
private:
public:
//Matrix data elements
float matrixData[9]={0.0};
//constructors
R4DMatrix3n();
R4DMatrix3n(float m0,float m3,float m6,float m1,float m4,float m7,float m2,float m5,float m8);
//copy constructors
R4DMatrix3n& operator=(const R4DMatrix3n& value);
//destructors
~R4DMatrix3n();
}
}
Just like in our Vector class, the data members of the matrix class are set to public. Doing so makes working with the engine a lot more cleaner. Please read Tips on developing a Math Engine for more information.
The implementation of the constructor is as follows:
R4DMatrix3n::R4DMatrix3n(){
// 3x3 matrix - column major. X vector is 0, 1, 2, etc. (openGL prefer way)
// 0 3 6
// 1 4 7
// 2 5 8
for (int i=0; i<9; i++) {
matrixData[i]=0.0f;
}
matrixData[0]=matrixData[4]=matrixData[8]=1.0f;
};
R4DMatrix3n::R4DMatrix3n(float m0,float m3,float m6,float m1,float m4,float m7,float m2,float m5,float m8){
// 3x3 matrix - column major. X vector is 0, 1, 2, etc. (openGL prefer way)
// 0 3 6
// 1 4 7
// 2 5 8
matrixData[0]=m0;
matrixData[3]=m3;
matrixData[6]=m6;
matrixData[1]=m1;
matrixData[4]=m4;
matrixData[7]=m7;
matrixData[2]=m2;
matrixData[5]=m5;
matrixData[8]=m8;
};
Notice the Column-major format of the matrix. Matrices have an arrangement property. They can be arranged in row-major format or column-major format. This is very important to keep in mind since multiplying vectors or matrices of wrong format will result in wrong calculations. OpenGL requires all matrices to be in column-major format.
Before we test our matrix class. Let's create a simple show() method. This method will print the value of the matrix components.
Add the following method in your implementation file:
//Make sure to include iostream
#include <iostream>
void R4DMatrix3n::show(){
// 3x3 matrix - column major. X vector is 0, 1, 2, etc. (openGL prefer way)
// 0 3 6
// 1 4 7
// 2 5 8
std::cout<<"["<<matrixData[0]<<","<<matrixData[3]<<","<<matrixData[6]<<","<<std::endl;
std::cout<<matrixData[1]<<","<<matrixData[4]<<","<<matrixData[7]<<","<<std::endl;
std::cout<<matrixData[2]<<","<<matrixData[5]<<","<<matrixData[8]<<"]"<<std::endl;
}
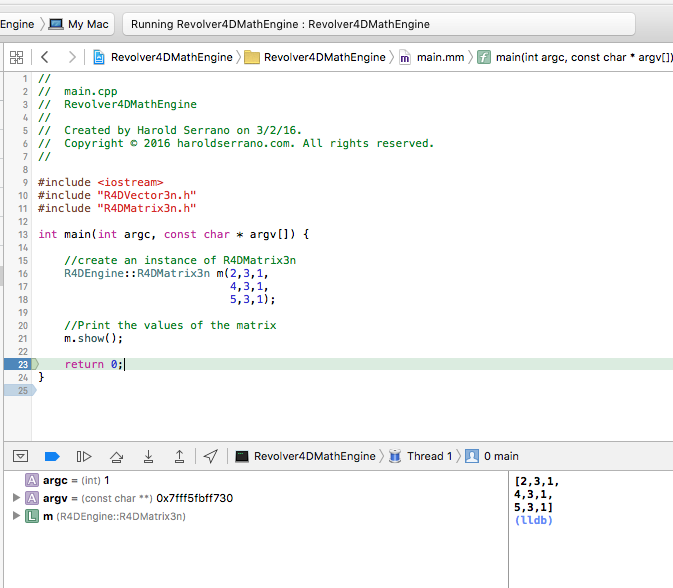
We are now ready to test our matrix class. In main.mm file, type the following:
#include <iostream>
#include "R4DVector3n.h"
#include "R4DMatrix3n.h"
int main(int argc, const char * argv[]) {
//create an instance of R4DMatrix3n
R4DEngine::R4DMatrix3n m(2,3,1,
4,3,1,
5,3,1);
//Print the values of the matrix
m.show();
return 0;
}
Press Command+B to build the project and run it. The output window should show the following:
Creating a Matrix Instance
Addition/Subtraction
Matrix addition/subtraction is allowed between matrices that have the same dimension. To add matrices simply add the corresponding components to each other.
For example:
Matrix addition is implemented as shown below. Notice that the components of each element is added together.
R4DMatrix3n R4DMatrix3n::operator+(const R4DMatrix3n &m) const{
R4DMatrix3n n;
// 3x3 matrix - column major. X vector is 0, 1, 2, etc. (openGL prefer way)
// 0 3 6
// 1 4 7
// 2 5 8
n.matrixData[0]=matrixData[0]+m.matrixData[0];
n.matrixData[3]=matrixData[3]+m.matrixData[3];
n.matrixData[6]=matrixData[6]+m.matrixData[6];
n.matrixData[1]=matrixData[1]+m.matrixData[1];
n.matrixData[4]=matrixData[4]+m.matrixData[4];
n.matrixData[7]=matrixData[7]+m.matrixData[7];
n.matrixData[2]=matrixData[2]+m.matrixData[2];
n.matrixData[5]=matrixData[5]+m.matrixData[5];
n.matrixData[8]=matrixData[8]+m.matrixData[8];
return n;
}
void R4DMatrix3n::operator+=(const R4DMatrix3n &m){
// 3x3 matrix - column major. X vector is 0, 1, 2, etc. (openGL prefer way)
// 0 3 6
// 1 4 7
// 2 5 8
matrixData[0]+=m.matrixData[0];
matrixData[3]+=m.matrixData[3];
matrixData[6]+=m.matrixData[6];
matrixData[1]+=m.matrixData[1];
matrixData[4]+=m.matrixData[4];
matrixData[7]+=m.matrixData[7];
matrixData[2]+=m.matrixData[2];
matrixData[5]+=m.matrixData[5];
matrixData[8]+=m.matrixData[8];
}
Let's test what we have. In the main.mm file, type the following:
#include <iostream>
#include "R4DVector3n.h"
#include "R4DMatrix3n.h"
int main(int argc, const char * argv[]) {
//create two instance of R4DMatrix3n
R4DEngine::R4DMatrix3n m(2,3,1,
2,1,4,
5,3,2);
R4DEngine::R4DMatrix3n n(5,3,2,
2,1,1,
5,3,2);
//add the matrices
R4DEngine::R4DMatrix3n p=m+n;
//Print the values of the matrix
p.show();
return 0;
}
Press Command+B to build the project and run it. The output window should show the following:
Matrix Addition Output
Scalar Multiplication
Scalar multiplication is performed by multiplying a scalar with each corresponding component in the matrix.
For example:
The implementation of matrix scalar multiplication is as follows:
R4DMatrix3n R4DMatrix3n::operator*(const float s) const{
// 3x3 matrix - column major. X vector is 0, 1, 2, etc. (openGL prefer way)
// 0 3 6
// 1 4 7
// 2 5 8
R4DMatrix3n n;
n.matrixData[0]=matrixData[0]*s;
n.matrixData[3]=matrixData[3]*s;
n.matrixData[6]=matrixData[6]*s;
n.matrixData[1]=matrixData[1]*s;
n.matrixData[4]=matrixData[4]*s;
n.matrixData[7]=matrixData[7]*s;
n.matrixData[2]=matrixData[2]*s;
n.matrixData[5]=matrixData[5]*s;
n.matrixData[8]=matrixData[8]*s;
return n;
}
void R4DMatrix3n::operator*=(const float s){
// 3x3 matrix - column major. X vector is 0, 1, 2, etc. (openGL prefer way)
// 0 3 6
// 1 4 7
// 2 5 8
matrixData[0]*=s;
matrixData[3]*=s;
matrixData[6]*=s;
matrixData[1]*=s;
matrixData[4]*=s;
matrixData[7]*=s;
matrixData[2]*=s;
matrixData[5]*=s;
matrixData[8]*=s;
}
Let's test these methods in main.mm
#include <iostream>
#include "R4DVector3n.h"
#include "R4DMatrix3n.h"
int main(int argc, const char * argv[]) {
//create two instance of R4DMatrix3n
R4DEngine::R4DMatrix3n m(7,6,3,
4,2,5,
10,6,4);
//Multiply matrix by sclar 3
R4DEngine::R4DMatrix3n p=m*3;
//Print the values of the matrix
p.show();
return 0;
}
Press Command+B and review the result of the scalar multiplication in the output window:
Matrix Scalar Multiplication
Multiplication
Unlike matrix addition, matrix multiplication does not require matrices to be of the same dimensions. However, the number of rows in matrix M must be equal to the number of colums in matrix N. For example:
For example:
Note an important propertry of matrices:
Thus, be careful when multiplying matrices. The order of multiplication matters.
Matrix multiplication is implemented as follows:
R4DMatrix3n R4DMatrix3n::operator*(const R4DMatrix3n& m) const{
// 3x3 matrix - column major. X vector is 0, 1, 2, etc. (openGL prefer way)
// 0 3 6
// 1 4 7
// 2 5 8
return R4DMatrix3n(matrixData[0]*m.matrixData[0]+ matrixData[3]*m.matrixData[1]+matrixData[6]*m.matrixData[2],
matrixData[0]*m.matrixData[3]+ matrixData[3]*m.matrixData[4]+matrixData[6]*m.matrixData[5],
matrixData[0]*m.matrixData[6]+ matrixData[3]*m.matrixData[7]+matrixData[6]*m.matrixData[8],
matrixData[1]*m.matrixData[0]+ matrixData[4]*m.matrixData[1]+matrixData[7]*m.matrixData[2],
matrixData[1]*m.matrixData[3]+ matrixData[4]*m.matrixData[4]+matrixData[7]*m.matrixData[5],
matrixData[1]*m.matrixData[6]+ matrixData[4]*m.matrixData[7]+matrixData[7]*m.matrixData[8],
matrixData[2]*m.matrixData[0]+ matrixData[5]*m.matrixData[1]+matrixData[8]*m.matrixData[2],
matrixData[2]*m.matrixData[3]+ matrixData[5]*m.matrixData[4]+matrixData[8]*m.matrixData[5],
matrixData[2]*m.matrixData[6]+ matrixData[5]*m.matrixData[7]+matrixData[8]*m.matrixData[8]);
}
void R4DMatrix3n::operator*=(const R4DMatrix3n& m){
// 3x3 matrix - column major. X vector is 0, 1, 2, etc. (openGL prefer way)
// 0 3 6
// 1 4 7
// 2 5 8
float t1;
float t2;
float t3;
t1=matrixData[0]*m.matrixData[0]+ matrixData[3]*m.matrixData[1]+matrixData[6]*m.matrixData[2];
t2=matrixData[0]*m.matrixData[3]+ matrixData[3]*m.matrixData[4]+matrixData[6]*m.matrixData[5];
t3=matrixData[0]*m.matrixData[6]+ matrixData[3]*m.matrixData[7]+matrixData[6]*m.matrixData[8];
matrixData[0]=t1;
matrixData[3]=t2;
matrixData[6]=t3;
t1=matrixData[1]*m.matrixData[0]+ matrixData[4]*m.matrixData[1]+matrixData[7]*m.matrixData[2];
t2=matrixData[1]*m.matrixData[3]+ matrixData[4]*m.matrixData[4]+matrixData[7]*m.matrixData[5];
t3=matrixData[1]*m.matrixData[6]+ matrixData[4]*m.matrixData[7]+matrixData[7]*m.matrixData[8];
matrixData[1]=t1;
matrixData[4]=t2;
matrixData[7]=t3;
t1=matrixData[2]*m.matrixData[0]+ matrixData[5]*m.matrixData[1]+matrixData[8]*m.matrixData[2];
t2=matrixData[2]*m.matrixData[3]+ matrixData[5]*m.matrixData[4]+matrixData[8]*m.matrixData[5];
t3=matrixData[2]*m.matrixData[6]+ matrixData[5]*m.matrixData[7]+matrixData[8]*m.matrixData[8];
matrixData[2]=t1;
matrixData[5]=t2;
matrixData[8]=t3;
}
Let's multiply two matrices together in main.mm:
#include <iostream>
#include "R4DVector3n.h"
#include "R4DMatrix3n.h"
int main(int argc, const char * argv[]) {
//create two instance of R4DMatrix3n
R4DEngine::R4DMatrix3n m(7,6,3,
4,2,5,
10,6,4);
R4DEngine::R4DMatrix3n p(3,2,1,
5,3,3,
4,2,1);
//Multiply matrices
R4DEngine::R4DMatrix3n n=m*p;
//Print the values of the matrix
n.show();
return 0;
}
Let's build the example code and review the result in the output window:
Matrix Multiplication
Identity Matrix
The Identity Matrix is a special kind of matrix which is similar to the concept of “1” in real numbers. Just like a real number multiplied by “1” results in the real number itself, any matrix multiply by the identity matrix results in the matrix itself.
The Identity matrix is defined as:
Multiplying any matrix by the identity matrix results in the same matrix.
Let's create a method which sets a matrix as an identity matrix:
void R4DMatrix3n::setMatrixAsIdentityMatrix(){
for (int i=0; i<9; i++) {
matrixData[i]=0.0f;
}
matrixData[0]=matrixData[4]=matrixData[8]=1.0f;
}
Let's test this method in main.mm:
#include <iostream>
#include "R4DVector3n.h"
#include "R4DMatrix3n.h"
int main(int argc, const char * argv[]) {
//create an instance of R4DMatrix3n
R4DEngine::R4DMatrix3n m(7,6,3,
4,2,5,
10,6,4);
//make the matrix an identity matrix
m.setMatrixAsIdentityMatrix();
//Print the values of the matrix
m.show();
return 0;
}
Build the project and review the result in the output window:
Matrix Identity
Inverse
In arithmetic, dividing a number by “4” is the same as multiplying a number by the inverse of “4”, i.e., “1/4”. Division operation does not exist in matrix arithmetic. However, it is possible to multiply a matrix by an inverse. The inverse of a matrix is denoted as:
When a matrix is multiplied by its inverse, it produces an identity matrix. Similar to when the real number “4” is multiplied by its inverse “1/4” produces “1”.
Keep in mind that not all matrices have an inverse.
The inverse of a matrix is implemented as follows:
void R4DMatrix3n::setMatrixAsInverseOfGivenMatrix(const R4DMatrix3n& m){
// 3x3 matrix - column major. X vector is 0, 1, 2, etc. (openGL prefer way)
// 0 3 6
// 1 4 7
// 2 5 8
float t1=m.matrixData[0]*m.matrixData[4];
float t2=m.matrixData[0]*m.matrixData[7];
float t3=m.matrixData[3]*m.matrixData[1];
float t4=m.matrixData[6]*m.matrixData[1];
float t5=m.matrixData[3]*m.matrixData[2];
float t6=m.matrixData[6]*m.matrixData[2];
//calculate the determinant
float det=(t1*m.matrixData[8]-t2*m.matrixData[5]-t3*m.matrixData[8]+t4*m.matrixData[5]+t5*m.matrixData[7]-t6*m.matrixData[4]);
//make sure the det is non-zero
if (det==0.0) return;
float invd=1.0f/det;
float m0=(m.matrixData[4]*m.matrixData[8]-m.matrixData[7]*m.matrixData[5])*invd;
float m3=-(m.matrixData[3]*m.matrixData[8]-m.matrixData[6]*m.matrixData[5])*invd;
float m6=(m.matrixData[3]*m.matrixData[7]-m.matrixData[6]*m.matrixData[4])*invd;
float m1=-(m.matrixData[1]*m.matrixData[8]-m.matrixData[7]*m.matrixData[2])*invd;
float m4=(m.matrixData[0]*m.matrixData[8]-t6)*invd;
float m7=-(t2-t4)*invd;
float m2=(m.matrixData[1]*m.matrixData[5]-m.matrixData[4]*m.matrixData[2])*invd;
float m5=-(m.matrixData[0]*m.matrixData[5]-t5)*invd;
float m8=(t1-t3)*invd;
matrixData[0]=m0;
matrixData[3]=m3;
matrixData[6]=m6;
matrixData[1]=m1;
matrixData[4]=m4;
matrixData[7]=m7;
matrixData[2]=m2;
matrixData[5]=m5;
matrixData[8]=m8;
}
R4DMatrix3n R4DMatrix3n::getInverseOfMatrix() const{
R4DMatrix3n result;
result.setMatrixAsInverseOfGivenMatrix(*this);
return result;
}
void R4DMatrix3n::invertMatrix(){
setMatrixAsInverseOfGivenMatrix(*this);
}
Let's test the inverse in main.mm:
#include <iostream>
#include "R4DVector3n.h"
#include "R4DMatrix3n.h"
int main(int argc, const char * argv[]) {
//create an instance of R4DMatrix3n
R4DEngine::R4DMatrix3n m(2,1,4,
3,4,1,
2,1,1);
//get the inverse
R4DEngine::R4DMatrix3n n=m.getInverseOfMatrix();
//Print the values of the matrix
n.show();
return 0;
}
Press Command+B to build the project. Review the result in the output window:
Matrix Inverse
Transpose
A Transpose operation takes each row of a matrix and converts it to a corresponding column. Mathematically, a transpose is represented as:
For example, the transpose of matrix M is done as follows:
Why would you need to transpose a matrix? A matrix can be represented as either a row-major or column-major matrix. During transformation operations, a vector and a matrix must be in either the same row-major or colum-major format. If they are not, the matrix must be transpose, so the results of the transformation are correct.
The transpose of a matrix is implemented as follows:
void R4DMatrix3n::setMatrixAsTransposeOfGivenMatrix(const R4DMatrix3n& m){
//3x3 Matrix
// 0 3 6
// 1 4 7
// 2 5 8
//3x3 transpose
// 0 1 2
// 3 4 5
// 6 7 8
matrixData[0]=m.matrixData[0];
matrixData[3]=m.matrixData[1];
matrixData[6]=m.matrixData[2];
matrixData[1]=m.matrixData[3];
matrixData[4]=m.matrixData[4];
matrixData[7]=m.matrixData[5];
matrixData[2]=m.matrixData[6];
matrixData[5]=m.matrixData[7];
matrixData[8]=m.matrixData[8];
}
R4DMatrix3n R4DMatrix3n::getTransposeOfMatrix() const{
R4DMatrix3n result;
result.setMatrixAsTransposeOfGivenMatrix(*this);
return result;
}
Let's test the transpose method in main.mm:
#include <iostream>
#include "R4DVector3n.h"
#include "R4DMatrix3n.h"
int main(int argc, const char * argv[]) {
//create an instance of R4DMatrix3n
R4DEngine::R4DMatrix3n m(2,1,4,
3,4,1,
2,1,1);
//get the transpose
R4DEngine::R4DMatrix3n n=m.getTransposeOfMatrix();
//Print the values of the matrix
n.show();
return 0;
}
Press Command+B to build the code. Review the result in the output window:
Matrix Transpose
Vector Transformation
One of the most important operations in Linear Algebra is the transformation space of a vector. Transformation refers to the act of rotating, scaling, skewing a vector. A transformation space occurs when a vector is multiplied by a matrix.
For example, a matrix representing a rotation about the x-axis is represented as follows:
To transform (rotate) a vector about the x-axis 90° counterclock-wise, you multiply the vector by the matrix:
Vector transformation is implemented in code as follows:
R4DVector3n R4DMatrix3n::operator*(const R4DVector3n & v) const{
// 3x3 matrix - column major. X vector is 0, 1, 2, etc. (openGL prefer way)
// 0 3 6
// 1 4 7
// 2 5 8
return R4DVector3n(matrixData[0]*v.x+matrixData[3]*v.y+matrixData[6]*v.z,
matrixData[1]*v.x+matrixData[4]*v.y+matrixData[7]*v.z,
matrixData[2]*v.x+matrixData[5]*v.y+matrixData[8]*v.z);
}
R4DVector3n R4DMatrix3n::transformVectorByMatrix(const R4DVector3n& v) const{
return (*this)*v;
}
Let's test the transformation in main.mm:
#include <iostream>
#include "R4DVector3n.h"
#include "R4DMatrix3n.h"
int main(int argc, const char * argv[]) {
//create an instance of R4DMatrix3n
R4DEngine::R4DMatrix3n m(0,0,0,
0,0,-1,
0,1,0);
//create an instance of vector R4DVector3n
R4DEngine::R4DVector3n v(0,1,0);
//transform the vector
R4DEngine::R4DVector3n v1=m*v;
//Print the value of the vector
v1.show();
return 0;
}
Finally, press Command+B to build the code. Review the results in the output window:
Vector Transformation
Source Code
The complete source code can be found here. Feel free to download it and play with it.